Réimaginer l’algorithme de tarification des transporteurs d’Uber Freight pour obtenir de meilleurs résultats

Par : Kenneth Chong (scientifique appliqué senior), Joon Ro (scientifique appliqué senior), Emir Poyraz (ingénieur senior) et May Wu (responsable des sciences appliquées).
Une version innovante d’un algorithme classique
Uber Freight exploite une place de marché bilatérale, qui s’interface séparément avec expéditeurs (qui cherchent à transporter des charges d’un point A à un point B) et avec les transporteurs (les chauffeurs de camion qui transportent ces charges). Les deux côtés de cette place de marché sont alimentés par des algorithmes de tarification dynamique. Chacune est structurée de manière légèrement différente en fonction des besoins du marché concerné.
Récemment, notre équipe a identifié le besoin de changer l’algorithme qui dicte la tarification des transporteurs. L’algorithme génère un taux basé sur une variété de facteurs tels que les conditions du marché, la taille du chargement, la distance à parcourir pour déplacer le chargement, etc. Jusqu’à présent, nous utilisions un algorithme basé sur les processus de décision de Markov (PDM) pour fixer les prix des transporteurs (voir cette page). article de blog précédent pour une description complète du fonctionnement du modèle MDP) parce qu’il est naturel pour notre problème : nous devons prendre des décisions de tarification de manière séquentielle dans le temps. Au fil du temps, nous nous sommes toutefois rendu compte que l’algorithme était certes performant, mais qu’il présentait des lacunes qu’il était difficile de combler avec une implémentation MDP standard.
Nous avons surmonté ces difficultés en
1) Troncature de l’induction à rebours
2) S’appuyer davantage sur l’apprentissage machine (ML) pour approximer la fonction de valeur.
3) Développement d’un nouvel algorithme de regroupement pour identifier les charges « similaires » qui peuvent être utiles pour l’estimation des coûts – en combinant de manière créative l’optimisation et le ML pour développer ce que nous pensons être une version plus robuste du MDP.
L’algorithme MDP est un choix naturel, mais sa mise en œuvre est difficile.
Pour illustrer brièvement le problème de la tarification des transporteurs, supposons que nous nous soyons engagés auprès du chargeur à transporter un chargement de Chicago (IL) à Dallas (TX). Le rendez-vous d’enlèvement commence exactement dans 5 jours : en d’autres termes, le délai d’exécution T est de 120 heures. Comme il est plus difficile de trouver des transporteurs dans un délai plus court, les prix ont tendance à augmenter lorsque le délai d’exécution diminue. Nous avons donc une séquence de décisions à prendre au fil du temps, que nous appelons une trajectoire de prix :
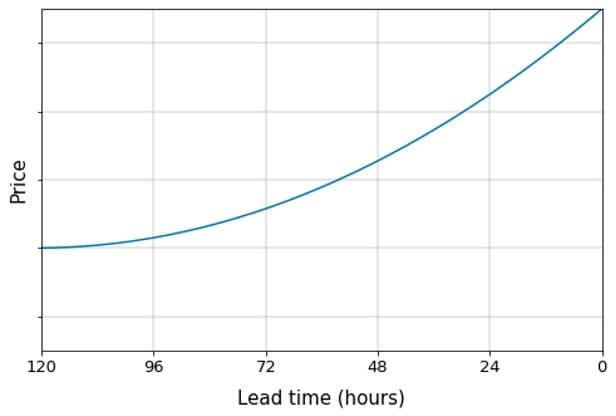
Figure 1 : Exemple de trajectoire de prix sur un délai de 5 jours
Comme nous actualisons les prix toutes les heures, cette trajectoire peut être représentée sous la forme d’une séquence {pt}t{T, T-1, …, 0}où pt est le prix offert t heures à partir de la prise en charge. L’objectif de notre algorithme est de choisir une trajectoire qui minimise, en espérance, le coût total pour couvrir la charge. Nous appelons cette quantité eCost:
eCostT=t=T0ptPr(Bt=1 | pt,St),
où Bt = 1 si la charge i est réservée au délai d’exécution t (0 sinon), et St désigne les variables d’état (éventuellement variables dans le temps) autres que le prix qui peuvent affecter la probabilité de réservation. Cette quantité augmente généralement au fur et à mesure que le temps passe et que le chargement reste sans réservation.
Dans le cadre d’une PDM, le calcul de l’eCost implique la résolution de l’équation de Bellman
Vt =minptPr(Bt | pt, St)pt +1-Pr(Bt | pt, St)Vt-1 t{0, 1, …, T}
Les quantités {Vt} sont directement interprétables en tant qu’eCost, sous réserve de notre politique de prix. Toutefois, l’estimation précise des probabilités de réservation constitue un élément essentiel de la PDM Pr(Bt=1 | pt , St). Bien que le modèle ML que nous utilisons à cet effet soit performant, les erreurs peuvent s’accumuler au fil du temps. Cela signifie que nous devenons vulnérables aux la malédiction de l’optimiseurqui stipule qu’en présence de bruit, les estimations du coût total associées à la décision optimale sont susceptibles d’être sous-estimées. Il en résulte des prix plus bas, trop optimistes, qui tendent à diminuer davantage lorsque les délais d’exécution sont plus longs.
En outre, la malédiction de la dimensionnalité présente des défis importants pour la modélisation de transitions d’état plus complexes. Par exemple, l’intégration de caractéristiques en temps quasi réel (NRT), telles que l’activité de l’application, dans nos prix implique de les ajouter aux variables d’état, ce qui rend rapidement notre problème infaisable d’un point de vue informatique.
Notre approche : un savant mélange de prédiction et d’optimisation
Pour améliorer la précision des prix, nous avons envisagé d’utiliser un modèle prédictif, plutôt qu’une induction à rebours standard, pour estimer l’eCost. En particulier, nous effectuons K ≤ T étapes d’induction à rebours, et si la charge n’est toujours pas réservée après K heures, nous substituons à la valeur de continuation VT-K une prédiction de ce modèle. Dans ce cas, les équations de Bellman deviennent :
Vt =minptPr(Bt | pt, St)pt +1-Pr(Bt | pt, St)Vt-1 t{T-K+1, …, T-1, T}
avec la condition limite
V
T-K
=eCos
t
T-K
.
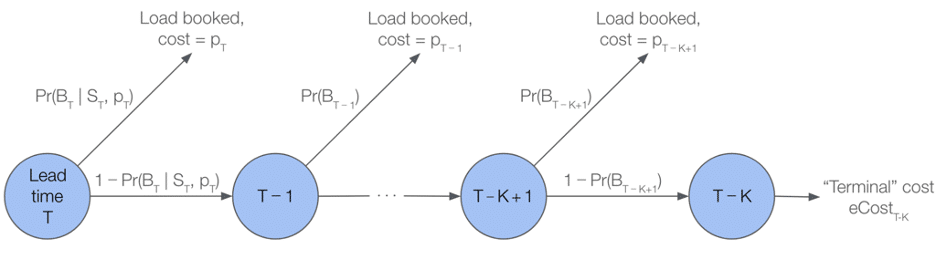
Figure 2 : Illustration de la prise de décision séquentielle dans le cadre d’un PDM
Le choix d’une valeur appropriée pour
K
a nécessité quelques itérations, mais cette rétro-induction tronquée permet d’atténuer chacun des problèmes que nous avons mis en évidence ci-dessus.
Un premier candidat pour un tel modèle prédictif était un ensemble XGBoost que nous avions déjà utilisé ailleurs pour la tarification des transporteurs. Les données d’apprentissage sont constituées de chargements historiques, de leurs caractéristiques (que nous décrivons plus en détail ci-dessous), des délais dans lesquels ils ont été comptabilisés, ainsi que de leurs coûts réalisés.
Cependant, les prédictions générées par ce modèle n’étaient pas adaptées à l’estimation de l’eCost pour deux raisons.
- Il y a une distinction importante à faire entre la durée de vie restante d’une charge et la durée de vie de la charge. restant d’une charge et son disponible délai d’exécution. Alors que nous inclurions les premiers dans le vecteur de caractéristiques au moment du service, il existe des schémas systématiques dans les seconds. En d’autres termes, des chargements similaires tendent à être disponibles à des moments précis. Par exemple, les longs trajets ont tendance à être disponibles dans des délais plus longs que les trajets plus courts. Ainsi, nous aurions des concentrations de points de données autour de certains délais disponibles, ce qui rendrait les prévisions moins fiables pour d’autres délais.
- Les données d’apprentissage se composaient uniquement de résultats – les réalisations de variables aléatoires, plutôt que leurs attentes – de sorte que les prédictions de ce modèle ne pouvaient pas non plus être interprétées comme un coût électronique. La manière de modifier l’ensemble d’apprentissage pour que les prédictions du modèle XGBoost puissent être traitées comme des attentes n’était pas évidente
Au lieu d’essayer de prédire directement l’eCost, nous empruntons les principes du clustering pour trouver un ensemble de charges similaires à celle à tarifer, et prendre une moyenne pondérée de leurs coûts totaux. Avec cette approche, les délais restants peuvent être explicitement incorporés dans l’eCost – nous pouvons exclure, de l’ensemble des chargements similaires, ceux qui ont été réservés plus tôt que le délai restant du chargement actuel. En outre, chacune des charges similaires identifiées peut être considérée comme un résultat potentiel pour la charge actuelle, auquel sont attribuées des probabilités égales aux poids utilisés dans le calcul de la moyenne.
Le principal défi consiste à développer un moyen de mesurer la similarité entre les charges, que nous décrivons à l’aide d’un certain nombre d’attributs :
- Emplacement des lieux d’enlèvement et de livraison
- Heure de la journée, jour de la semaine où le chargement doit être enlevé ou livré
- Conditions du marché au moment où le chargement doit être déplacé
Il y a un mélange de caractéristiques continues et catégorielles, et il n’est pas du tout évident de savoir comment les pondérer les unes par rapport aux autres lors du calcul de la similarité.
…avec un algorithme de regroupement non conventionnel
Nous avons développé un nouvel algorithme dans lequel notre modèle XGBoost susmentionné est utilisé pour effectuer le regroupement. Prenons le cas simple où notre modèle est un arbre de décision unique (peu profond) avec une seule caractéristique : la distance de conduite. Nous pourrions obtenir un arbre comme le suivant :
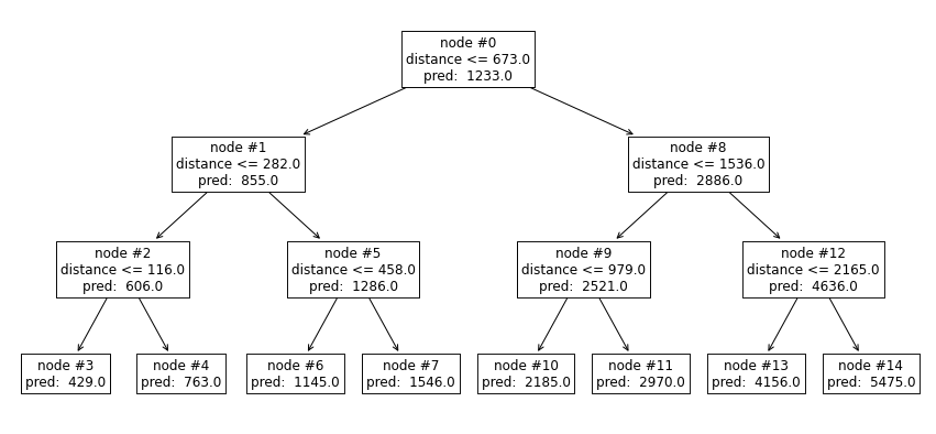
Figure 3 : Illustration d’un arbre de décision unique pour le regroupement
Deux charges peuvent être considérées comme « similaires » si leurs prédictions sont faites à partir du même nœud feuille. Dans le cas du nœud feuille n°6, nous savons que les distances d’acheminement sont toutes deux comprises entre 282 et 458 miles.
Cela peut sembler une façon rudimentaire de mesurer la similarité, mais en développant des arbres de décision plus profonds et en incorporant davantage de caractéristiques, nous exigeons que les deux charges aient des valeurs comparables sur un certain nombre de dimensions pour être considérées comme « similaires ». Nous pouvons différencier davantage en cultivant des arbres supplémentaires. En bref, nous associons à chaque charge un vecteur d’intégration, composé de nonzéros aux emplacements correspondant aux nœuds feuilles dans lesquels la charge tombe. Nous mesurons la similarité entre les charges par la similarité en cosinus de leur intégration, qui est directement liée au nombre d’arbres dans lesquels les deux ont des nœuds feuilles communs.
La fluidité des prix a permis d’améliorer les résultats des réservations
Compte tenu des changements relativement importants que nous avons apportés à l’algorithme, nous avons procédé à un déploiement en deux phases principales. Tout d’abord, nous avons intégré eCost dans les algorithmes utilisés dans les canaux de réservation secondaires, et nous avons effectué un test A/B pour nous assurer qu’il n’y avait pas de baisse de performance. Deuxièmement, nous avons réalisé une expérience d’inversion en la comparant à la version précédente de MDP. L’effet net de ces deux expériences a été une réduction statistiquement significative du coût total de la couverture des charges, sans impact négatif sur les indicateurs secondaires. Nous attribuons ce résultat aux trajectoires de prix plus lisses générées par le nouvel algorithme, qui permet de réserver les charges plus tôt dans leur cycle de vie. Ce point est particulièrement important, car les coûts ont tendance à augmenter fortement dès que les délais d’exécution tombent en dessous de 24 heures.
Le déploiement de ce nouvel algorithme s’accompagne d’un certain nombre d’avantages secondaires. La réservation anticipée des chargements, grâce à des trajectoires de prix plus lisses, permet non seulement de réduire les coûts, mais aussi d’éviter les fortes augmentations de coûts associées à des délais plus courts. La réduction du coût total de couverture des chargements nous permet d’offrir des prix plus compétitifs aux expéditeurs, ce qui, à son tour, augmente le volume. En outre, des trajectoires de prix plus plates pourraient inciter les transporteurs à vérifier les chargements sur l’application plus tôt dans leur cycle de vie. Au-delà de ces avantages commerciaux, l’algorithme a également contribué à réduire la dette technique en unifiant la tarification entre les canaux de réservation, ainsi qu’en supprimant les composants non essentiels utilisés dans l’implémentation précédente de MDP.
Bien que nous pensions qu’il y ait encore des domaines à améliorer, ce nouvel algorithme de tarification fournit un modèle de la façon dont le PDM peut être appliqué à de nouveaux cas d’utilisation au sein d’Uber Freight.
*Puisque nous utilisons également eCost comme une sorte d’approximation de la fonction de valeur, le problème que nous allons résoudre présente quelques similitudes avec un
programme dynamique approximatif
.



