Reimaginar el algoritmo de precios de Uber Freight para obtener mejores resultados

Por: Kenneth Chong (Científico Aplicado Sr.), Joon Ro (Científico Aplicado Sr.), Emir Poyraz (Ingeniero Sr.) y May Wu (Directora de Ciencias Aplicadas)

Un giro innovador a un algoritmo clásico

Uber Freight opera un mercado de dos caras, que interactúa por separado con cargadores (que buscan mover cargas del punto A al punto B) y con los transportistas (camioneros que trasladan estas cargas). Ambos lados de este mercado funcionan con algoritmos de precios dinámicos. Cada una de ellas está estructurada de forma diferente en función de las necesidades de cada mercado.

Recientemente, nuestro equipo identificó la necesidad de cambiar el algoritmo que dicta los precios de los transportistas. El algoritmo genera una tarifa en función de diversos factores, como las condiciones del mercado, el tamaño de la carga, la distancia que hay que recorrer para moverla, etcétera. Hasta ahora, utilizábamos un algoritmo basado en procesos de decisión de Markov (MDP) para fijar los precios de los transportistas (véase este entrada anterior del blog para una descripción completa de cómo funciona el modelo MDP) porque es natural para nuestro problema: necesitamos tomar decisiones de fijación de precios secuencialmente a lo largo del tiempo. Sin embargo, con el tiempo nos dimos cuenta de que, aunque el algoritmo era eficaz, tenía deficiencias que resultaban difíciles de solucionar con una implementación MDP estándar.

Los superamos:

1) Truncar la inducción hacia atrás

2) Recurrir en mayor medida al aprendizaje automático para aproximar la función de valor.

3) Desarrollar un nuevo algoritmo de agrupación para identificar cargas «similares» que puedan ser útiles para estimar el coste: combinar de forma creativa la optimización y el ML para desarrollar lo que creemos que es una versión más robusta del MDP.

MDP es una elección natural de algoritmo, pero su implementación es un reto

Para ilustrar brevemente el problema de la fijación de precios del transportista, supongamos que nos hemos comprometido con el cargador a transportar una carga desde Chicago (Illinois) a Dallas (Texas). La cita de recogida comienza exactamente dentro de 5 días: en otras palabras, el plazo de entrega T es de 120 horas. Como resulta más difícil encontrar transportistas con menos antelación, los precios tienden a aumentar a medida que disminuye el plazo de entrega. Así pues, tenemos una secuencia de decisiones que tomar a lo largo del tiempo, que denominamos trayectoria de precios:

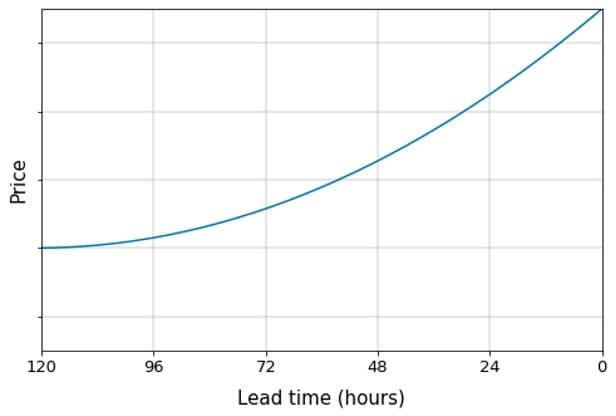
Figura 1: Ejemplo de trayectoria de precios en un plazo de 5 días

Dado que actualizamos los precios cada hora, esta trayectoria puede representarse como una secuencia {pt}t{T, T-1, …, 0}donde pt es el precio ofrecido t horas desde la recogida. El objetivo de nuestro algoritmo es elegir una trayectoria que minimice, en expectativa, el coste total para cubrir la carga. Denominamos a esta cantidad eCost:

eCostT=t=T0ptPr(Bt=1 | pt,St),

donde Bt = 1 si la carga i está reservada en el ciclo de fabricación t (0 en caso contrario), y St denota variables de estado (posiblemente variables en el tiempo) distintas del precio que pueden afectar a la probabilidad de reserva. Esta cantidad suele aumentar a medida que pasa el tiempo y la carga sigue sin reservarse.

Con MDP, calcular el eCost implica resolver la ecuación de Bellman

Vt =minptPr(Bt | pt, St)pt +1-Pr(Bt | pt, St)Vt-1 t{0, 1, …, T}

Las cantidades {Vt} son directamente interpretables como eCost, condicionados a nuestra política de precios. Sin embargo, un elemento crucial de la MDP es la estimación precisa de las probabilidades de reserva. Pr(Bt=1 | pt , St). Aunque el modelo ML que utilizamos para ello funciona bien, los errores pueden acumularse con el tiempo. Esto significa que nos volvemos vulnerables a la la maldición del optimizadorque afirma que, en presencia de ruido, es probable que las estimaciones de los costes totales asociados a la decisión óptima estén infravaloradas. Esto, a su vez, conduce a precios más bajos y excesivamente optimistas que tienden a disminuir aún más con plazos de entrega más largos.

Además, la maldición de la dimensionalidad presenta retos importantes a la hora de modelar transiciones de estado más complejas. Por ejemplo, la incorporación de características en tiempo casi real (NRT), como la actividad de la aplicación, a nuestros precios implica añadirlas a las variables de estado, lo que rápidamente hace que nuestro problema sea inviable desde el punto de vista computacional.

Nuestro enfoque: una cuidadosa combinación de predicción y optimización

Para mejorar la precisión de los precios, exploramos el uso de un modelo predictivo, en lugar de una inducción hacia atrás estándar, para estimar el eCost. En concreto, realizamos K ≤ T etapas de inducción hacia atrás, y si la carga sigue sin reservarse después de K horas, sustituimos por el valor de continuación VT-K una predicción de este modelo. En este caso, las ecuaciones de Bellman se convierten en:

Vt =minptPr(Bt | pt, St)pt +1-Pr(Bt | pt, St)Vt-1 t{T-K+1, …, T-1, T}

con la condición de contorno
V
T-K
=eCos
t
T-K
.

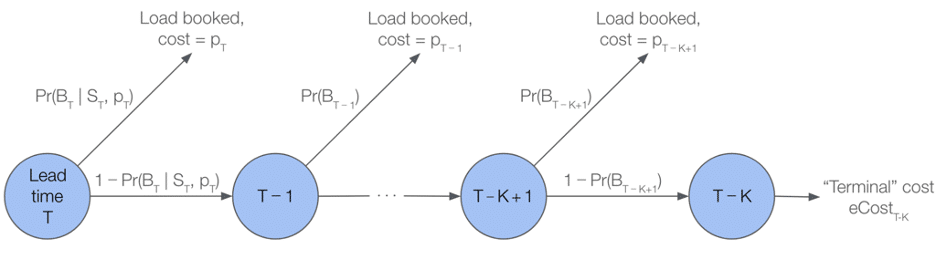
Figura 2: Ilustración de la toma de decisiones secuencial en MDP

Elegir un valor adecuado para
K
requirió alguna iteración, pero esta inducción hacia atrás truncada ayuda a mitigar cada uno de los problemas que destacamos anteriormente.

Un candidato inicial para este modelo predictivo era un conjunto XGBoost que ya habíamos utilizado anteriormente en la fijación de precios de las aerolíneas. Los datos de entrenamiento consistían en cargas históricas, sus características (que describimos con más detalle a continuación), los plazos en los que se reservaron, así como sus costes realizados.

Sin embargo, las predicciones generadas por este modelo no eran adecuadas para estimar el eCost por dos razones.

1. Hay que hacer una distinción importante entre la carga restante de una carga y su disponible plazo de entrega. Aunque incluiríamos los primeros en el vector de características en el momento de servir, existen patrones sistemáticos en los segundos. Es decir, cargas similares tienden a estar disponibles en determinados plazos. Por ejemplo, los trayectos más largos suelen estar disponibles en plazos más largos que los cortos. Así, tendríamos concentraciones de puntos de datos en torno a determinados plazos disponibles, lo que haría menos fiables las predicciones en otros plazos.
2. Los datos de entrenamiento consistían únicamente en resultados -las realizaciones de variables aleatorias, en lugar de sus expectativas-, por lo que las predicciones de este modelo tampoco podían interpretarse como un eCost. No estaba claro cómo modificar el conjunto de entrenamiento para que las predicciones del modelo XGBoost pudieran tratarse como expectativas.

En lugar de intentar predecir el eCost directamente, tomamos prestados los principios de la agrupación para encontrar un conjunto de cargas que sean similares a la que se va a tarificar, y tomamos una media ponderada de sus costes totales. Con este enfoque, los plazos de entrega restantes pueden incorporarse explícitamente al eCost: podemos excluir, del conjunto de cargas similares, las que se reservaron antes del plazo de entrega restante de la carga actual. Además, cada una de las cargas similares identificadas puede considerarse como un resultado potencial de la carga actual, al que se asignan probabilidades iguales a las ponderaciones utilizadas en la promediación.

El principal reto aquí es desarrollar una forma de medir la similitud entre las cargas, que describimos con una serie de atributos:

• Ubicación de las instalaciones de recogida y entrega
• Hora del día, día de la semana en que está prevista la recogida o entrega de la carga
• Condiciones del mercado en la fecha prevista para el traslado de la carga

Hay una mezcla de características continuas y categóricas, y no está nada claro cómo deben ponderarse entre sí a la hora de calcular la similitud.

…con un algoritmo de agrupación poco convencional

Hemos desarrollado un nuevo algoritmo en el que se utiliza nuestro modelo XGBoost antes mencionado para realizar la agrupación. Consideremos el caso simple en el que nuestro modelo es un único árbol de decisión (poco profundo) con una única característica: la distancia de conducción. Podríamos obtener un árbol como el siguiente:

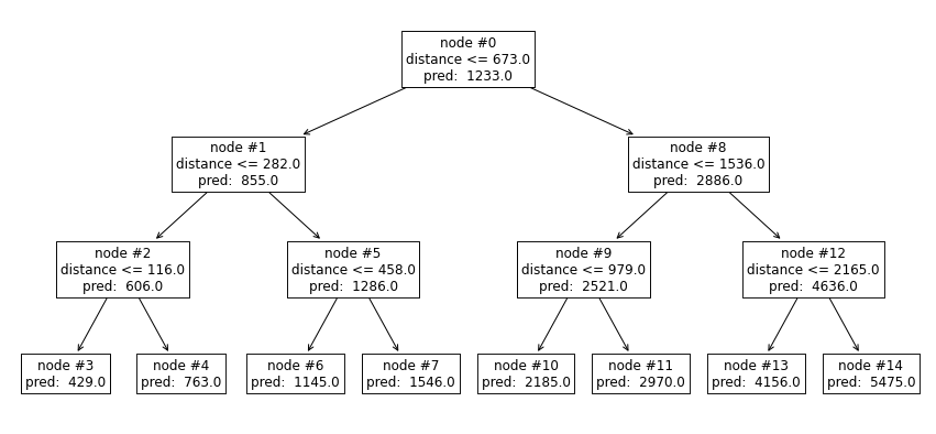
Figura 3: Ilustración de un único árbol de decisión para la agrupación

Dos cargas pueden considerarse «similares» si sus predicciones se realizan desde el mismo nodo hoja. En el caso del nodo hoja nº 6, sabemos que sus distancias de ruta están ambas entre 282 y 458 millas.

Puede parecer una forma burda de medir la similitud, pero al hacer crecer árboles de decisión más profundos e incorporar más características, exigimos que las dos cargas tengan valores comparables en una serie de dimensiones para considerarlas «similares». Podemos diferenciarnos aún más cultivando árboles adicionales. En pocas palabras, asociamos a cada carga un vector de incrustación, formado por nonzeros en ubicaciones que coinciden con los nodos hoja en los que cae la carga. Medimos la similitud entre cargas a través de la similitud coseno de sus incrustaciones, que está directamente relacionada con el número de árboles en los que ambas tienen nodos hoja comunes.

Precios más asequibles y mejores resultados en las reservas

Dados los cambios bastante sustanciales que introdujimos en el algoritmo, realizamos un despliegue en dos fases principales. En primer lugar, incorporamos eCost a los algoritmos que utilizamos en los canales de reserva secundarios, y realizamos una prueba A/B para asegurarnos de que no disminuyera el rendimiento. En segundo lugar, realizamos un experimento de conmutación comparándolo con la versión anterior de MDP. El efecto neto de estos dos experimentos fue una reducción estadísticamente significativa del coste total de la cobertura de cargas, sin ningún impacto negativo en las métricas secundarias. Lo atribuimos a las trayectorias de precios más suaves generadas por el nuevo algoritmo, que hace que las cargas se reserven antes en sus ciclos de vida. Esto es especialmente relevante, ya que los costes tienden a aumentar bruscamente una vez que los plazos de entrega caen por debajo de las 24 horas.

Con el despliegue de este nuevo algoritmo llegan una serie de beneficios secundarios. La reserva anticipada de cargas, debida a trayectorias de precios más suaves, no sólo reduce los costes, sino que es crucial para evitar los bruscos aumentos de costes asociados a plazos de entrega más cortos. La reducción del coste total para cubrir las cargas nos permite ofrecer precios más competitivos a los cargadores, lo que, a su vez, aumenta el volumen. Además, las trayectorias de precios más planas podrían llevar a los transportistas a comprobar las cargas en la aplicación antes en sus ciclos de vida. Más allá de estas ventajas comerciales, el algoritmo también ha contribuido a reducir la deuda técnica al unificar los precios en todos los canales de reserva, así como al eliminar componentes no esenciales utilizados en la anterior implementación de MDP.

Aunque creemos que hay áreas en las que se puede seguir mejorando, este nuevo algoritmo de fijación de precios proporciona un modelo de cómo se puede aplicar la MDP a nuevos casos de uso dentro de Uber Freight.

*Dado que también estamos utilizando eCost como una especie de aproximador de la función de valor, el problema que resolvemos ahora comparte algunas similitudes con un
programa dinámico aproximado
.